在华电附近打印材料时发现一露天二手书贩卖教材,价格尚可遂买几本常用工具书.正好最近遇到一点算法小问题,尝试整理一下.
1. 两个栈实现队列
栈的特性是FILO,队列的特性是FIFO,最直接的思路就是利用两个栈来回倒腾.当出栈的时候,将一个队列的所有元素倒腾到另外一个栈中.总会有一个栈是空的,这样①控制好每次操作哪个栈,②每次操作栈需不需要reverse 即可. 后来发现比较繁琐,需要记录很多标志位,遂放弃.
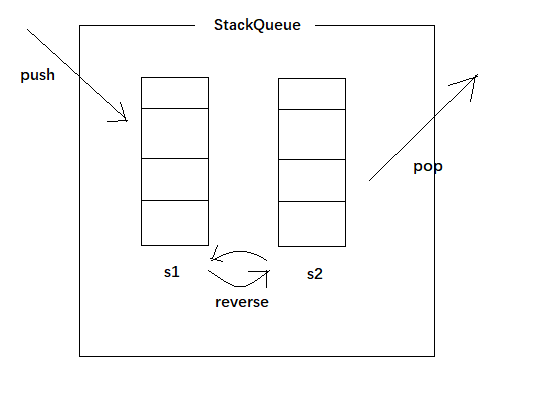
在力扣看到种比较简单的写法,其比较趋向将两个栈区分开,一个总是push(),另一个总是pop(), 大致的想法就是,每次我都从s2中pop,一旦s2为空,说明之前的一波已经pop完了, 需要从s1中全部倒腾过来,这样s2相当于一个buffer,为空时都去获取时序最前的那一部分s1中的元素,并将顺序倒放,不为空时,直接从s2中pop(),顺序正好是对的. 思路比较巧妙,效率也很高. 如图 :

// 代码示意
public class StackQueue<T>{
private Stack s1 = new Stack<T>();
private Stack s2 = new Stack<T>();
public void push( T t){
s1.push(t);
}
public T pop(){
if(s2.isEmpty()){
while(!s1.isEmpty){
s2.push(s1.pop());
}
}
return s2.pop();
}
}
2. 蛇形打印二叉树
题目 : 按照图示绿色轨迹打印二叉树.
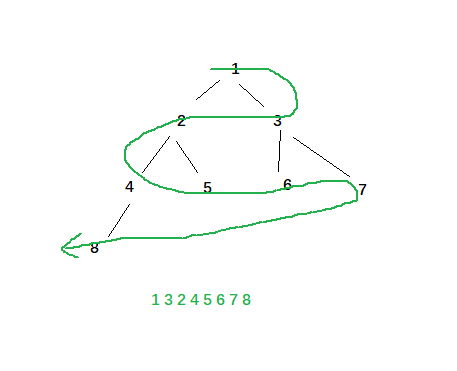
背景 : 广度优先和深度优先遍历: 我个人觉得一般树遍历使用深度优先遍历(如递归遍历)很容易理解也很直观,元操作所需要的临时存储会被递归的形参隐式的创建,直到递归结束再统一归还,是很方便的.非递归则使用栈来存储元操作所需要临时存储的数据; 广度优先遍历也需要显示借助额外的数据结构来缓存这些元操作数据. 事实上他们所占用的资源时类似的. 但是由于递归对于资源的占用不直接受人为控制,容易出现严重资源错误,并不被推荐使用.
这个问题是广度优先遍历的一个变种,在打印每一行的时候加了一个简单的标志位,用于控制每一行的打印顺序.
// 代码示意
// 定义节点
class TreeNode{
Inteeger value;
TreeNode left;
TreeNode right;
}
// 蛇形打印类
public class SnakePrint{
public static snackPrint(TreeNode node){
Queue Q = new Queue();
List<Integer> resultList = new ArrayList<>();
Q.add(node);
int size = Q.size();
boolean isNeedReverse = true;
while(Q.isNotEmpty()){
List<Integer> temp = new ArrayList<>();
for(int i = 0; i<size;i++){
TreeNode currentNode = Q.poll();
temp.add(isNeedReverse ? (0,currentNode.value) : currentNode.value);
if(currentNode.left != null ){
Q.add(currentNode.left);
}
if(currentNode.right != null ){
Q.add(currentNode.right);
}
}
resultList.addAll(temp);
}
return resultList;
}
}
3. 一点思考
可以大概看到,题目1到题目2,从一重循环到二重循环,思考的复杂度有些递增.如果没有玩儿过这种脑筋急转弯没接触过类似训练的话,上来就嗑,很有可能会无从下手,因为连最基本的API都不知道. 就算知道意思和思路,但是下笔就是不知道怎么写,茶壶煮饺子--倒不出来.可是有个问题:我们为什么要做这方面的训练呢,换句话说我们为什么要有解这种问题的能力呢?
我的想法是 : 算法这种东西,它内在的各种技巧性的东西并不是有强关联性的,很难短时间内形成强逻辑性的知识体系. 算法中的思维火花散落在很多角落,但是也不是无迹可寻. 我们在练习的时候会把这些散落的火花捡起来,分类整理和归纳,到最后对每个大致的分类达到一个比较熟练的程度.当然也有这方面有比较有天赋的童鞋思维本身很活跃不用做这些训练,能很快的找到问题的解决办法.事实上,我认为这些经典算法之所以流传至今,是因为这是很多前辈的智慧结晶.随着理论,材料等发展,更加先进的算法也会更迭,已经不是靠个人智慧的时代了.知识的积累本身是一种熵减的过程.好在大部分基础科学及其衍生学科知识是成体系的,比较容易学习.当然也有暂时没有形成体系的或者体系比较弱的.当知识的累积量达到了一个人皓首所不能掌握的时候(事实上我觉得现有知识的总量已经达到了...) . 当单一学科的累积量,细分领域的研究也达到了瓶颈处,在天花板下,应该会有新的进化方向出现吧 ...(扯远了)
熟练不是最终目的,最终的目的是通过掌握这些技巧锻炼我们的思维,使我们在解决实际问题的时候能更加高效快速的找到问题的答案.




评论区