算法练习(4) - 最大子数组

1 分治法

问题分析思路
将 数组 a[i...j]进行近二等分为2个子数组: a[i...mid] , a[mid+1 ... j];

设最大子数组的下标为 left,right,那么left ,right 的分布情况只能有三种 :

• i <= left < right <= mid
• mid+1 <= left < right <= j
• i <= left <= mid <= right <= j
  即 left 和 right 要么都在mid左边,要么都在mid右边,或者一个在左边,一个在右边;
  那么接下来我们看一下,将数组完全二分后,求解思路:

先将数组进行二分

可以看到,分解后最小问题为单元素求解,最大子数组即为其自身;

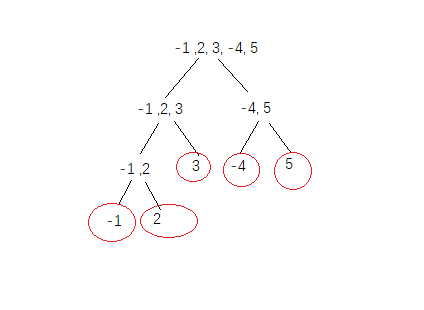
到第二级时(此时数组只有2个元素),且已知左子数组的 最大子数组 和 右子数组的最大子数组,那么只剩下求解left 和 right 跨mid 的情况了;

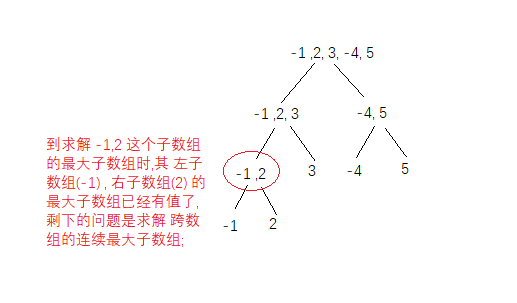
同理, 我们可以再往上看一级

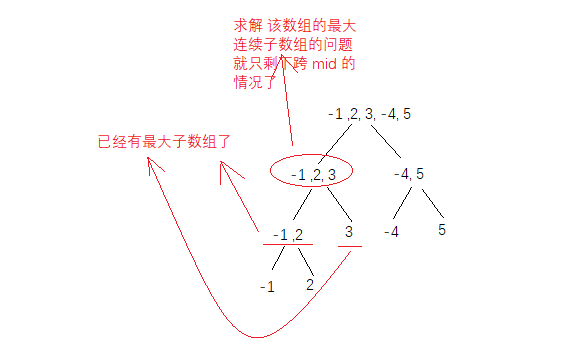
以此类推,我们可以知道,实际上最后的问题都转化为了 跨 mid的结果 与 二分后的左右子数组的最大子数组的2个结果 三个之中作比较取最大值,而 左右子数组的最大子节点到最后又转化为了单节点,所以最终问题转化为了 跨mid情况的求解;

package top.buukle.buukle._03MaxSubarray;

import org.junit.Test;

public class MaxSubarray {

    @Test
    public void mergeSort_test() {
        Integer[] A = {13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7};
        Result maxSubarray = findMaxSubarray(A, 0, A.length - 1);
        System.out.println(maxSubarray);
    }

    private Result findMaxSubarray(Integer[] a, int low, int high) {
        if(low == high){
            Result result = new Result();
            result.maxValue = a[low];
            result.left = low;
            result.right = high;
            return result;
        }
        int middle =( low +high) / 2;
        Result maxSubarrayLeft = findMaxSubarray(a, low, middle);
        Result maxSubarrayRight = findMaxSubarray(a, middle + 1, high);
        Result maxSubarrayCross = findMaxSubMax(a, low, middle, high);
        if(maxSubarrayLeft.maxValue >= maxSubarrayRight.maxValue && maxSubarrayLeft.maxValue >= maxSubarrayCross.maxValue ){
            return maxSubarrayLeft;
        }else  if(maxSubarrayRight.maxValue >= maxSubarrayLeft.maxValue && maxSubarrayRight.maxValue >= maxSubarrayCross.maxValue ){
            return maxSubarrayRight;
        }else {
            return maxSubarrayCross;
        }
    }

    private Result findMaxSubMax(Integer[] a, int low, int middle, int high) {

        int sumLeft = 0;
        int maxLeft = 0;
        int piLeft = middle;
        for(int i = middle; i>=low ;i--){
            sumLeft +=a[i];
            if(sumLeft > maxLeft){
                piLeft = i;
                maxLeft = sumLeft;
            }
        }
        int sumRight = 0;
        int maxRight = 0;
        int piRight = middle;
        for(int i = middle + 1; i<= high ;i ++ ){
            sumRight +=a[i];
            if(sumRight > maxRight){
                piRight = i;
                maxRight = sumRight;
            }
        }
        Result result = new Result();
        result.maxValue = maxRight + maxLeft;
        result.left = piLeft;
        result.right = piRight;
        return result;
    }

    class Result {
        int left;
        int right;
        int maxValue;

        @Override
        public String toString() {
            return "Result{" +
                    "left=" + left +
                    ", right=" + right +
                    ", maxValue=" + maxValue +
                    '}';
        }
    }
}

贪心法

使用一个变量来记录所有的加和,这个加和一旦为负数,及抛弃前面所有的数据,重新开始计算求和,中间记录最大的和即为目标值,在赋值max时和sum清零时,即为 right索引和left索引更新的时机;

package top.buukle.buukle._03Greedy;

import org.junit.Test;

public class MaxSubarraySum {

    @Test
    public void MaxSubarray_test() {
        Integer[] A = {13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7};
        int maxSubarraySum = findMaxSubarray(A);
        System.out.println(maxSubarraySum);
    }

    private Integer findMaxSubarray(Integer[] a) {
        int sum=0;
        int max = Integer.MIN_VALUE;
        int left = 0;
        int right =0;
        for(int i =0;i<a.length;i++){
            sum = sum + a[i];
            if(sum > 0){
                if(sum > max ){
                    max = sum;
                    right = i;
                }
            }
            else{
                sum = 0;
                left = i+1;
            }
        }
        System.out.println(left+"--" +right);
        return max;
    }

}